#116 - Red, green or blue tiles
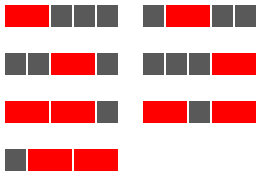
A row of five grey square tiles is to have a number of its replaced with coloured oblong tiles chosen from red (length two), green (length three), or blue (length four).
If red tiles are chosen there are exactly seven ways this can be done.
If green tiles are chosen there are three ways.
And if blue tiles are chosen there are two ways.
Assuming that colours cannot be mixed there are 7 + 3 + 2 = 12 ways of replacing the grey tiles in a row measuring five units in length.
How many different ways can the grey tiles in a row measuring fifty units in length be replaced if colours cannot be mixed and at least one coloured tile must be used?
This is related to #117 - Red, green, and blue tiles
This is also related to both #114 - Counting block combinations I and #115 - Counting block combinations II. Unlike those problems, we should not include the configuration of all black tiles. Additionally, each colored tile is a specific length.
Since the tiles can’t mix, this actually makes things relatively simple. We keep three separate arrays, one for each color. Since the tiles are constant lengths, we slide it along and calculate the ways to fill the remaining black tiles to the left. In summary, our code is very similar to both 114 and 115 with some slight modifications.
# file: "problem116.py"
targetN = 50
# Red, blue, and green tiles can't be mixed
# so create three separate arrays
# No space of at least one so smallest value is n = 0
# Order is red, green, blue. The size would be the index + 2
coloredTiles = np.zeros((3, targetN+1), dtype=np.uint64)
coloredTiles[:, :2] = 1
# Use dynamic programming to find
# the number for each n of each color
for n in range(2, targetN+1):
for i in range(len(coloredTiles)):
size = i + 2
blackSpaceLeft = np.arange(n - size + 1)
coloredTiles[i, n] = np.sum(coloredTiles[i, blackSpaceLeft]) + 1
# Subtract 3 to remove the all-black config
# axis=0 means to sum column by column.
totalTiles = np.sum(coloredTiles, axis=0) - 3
print(totalTiles[-1])
Running this code results in an output of,
20492570929
0.003920800000000002 seconds.
Thus, if mixing colors are prohibited, then there are 20492570929 ways to fill a row that is 50 units long.