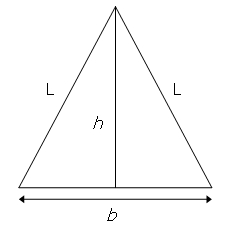#138 - Special isosceles triangles
Consider the isosceles triangle with base length, $b=16$, and legs, $L=17$.
By using the Pythagorean theorem it can be seen that the height of the triangle, $h=\sqrt{17^2-8^2}=15$, which is one less than the base length.
With $b=272$ and $L=305$, we get $h=273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h=b\pm1$.
Find $\sum L$ for the twelve smallest isosceles triangles for which $h=b\pm1$ and $b,L$ are positive integers.
Whenever you drop the height of an isosceles triangle down to the base, it cuts the base in two and produces two right triangles, whose leg lengths are $b/2$ and $h$, with hypotenuse $L$. Since we want $h=b\pm1$, then $b/2<h$.
Let’s say that $\alpha=h$, $\beta=b/2$, and $\gamma=L$. To have our original property hold, we need to find Pythagorean triples such that $2\beta=\alpha\pm1$. Additionally, this also means the triples have to be primitive, because if they weren’t, the difference would be greater than 1. We can use the Pythaogrean tree as we did in previous problems.
Looking at the tree, the two solutions given in the problem correspond to the (15, 8, 17) and (273, 136, 305) triangles. It seems we multiplied by $C$ for the first triple, then multiplied by $B$ then $C$ to get the second one. Does this pattern hold? If we multiply by $CB$ on the left again, let’s see if we get another solution. \[(CB)^2C\overrightarrow{v} = \begin{bmatrix} -545 & 610 & 818 \\ -274 & 305 & 410 \\ -610 & 682 & 915 \end{bmatrix} \begin{bmatrix} 3 \\ 4 \\ 5 \end{bmatrix} = \begin{bmatrix} 4895 \\ 2448 \\ 5473 \end{bmatrix}\]
Indeed, we have 2(2448) = 4896, which is one more than 4895. To prove this pattern works, one would need to go through the multiplication with a generic triple $(\alpha, \beta, \gamma)$ and show that the rule holds with $CB$ and not with any other pair.
The only code is to define the matrics and multiply them together, which is quick and easy with numpy.
# file: "problem138.py"
B = np.array([
[1, 2, 2],
[2, 1, 2],
[2, 2, 3]
], dtype=object)
C = np.array([
[-1, 2, 2],
[-2, 1, 2],
[-2, 2, 3]
], dtype=object)
baseTriple = np.array([15, 8, 17], dtype=object)
CBprod = np.dot(C, B)
sumL = 17
limit = 12
for _ in range(limit - 2):
CBprod = np.dot(np.dot(C, B), CBprod)
triple = np.dot(CBprod, baseTriple)
sumL += triple[-1]
print(sumL)
Running this short loop, we get
1118049290473627
0.00019860000000002098 seconds.
Thus, the sum of all hypotenuses is 1118049290473627.