#173 - Using up to one million tiles how many different 'hollow' square laminae can be formed?
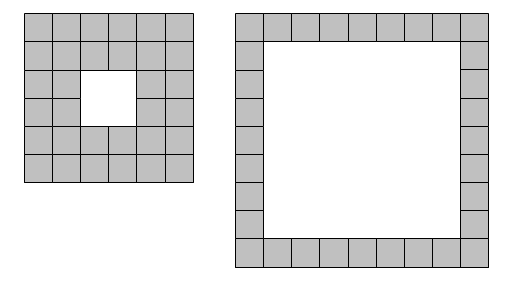
We shall define a square lamina to be a square outline with a square “hole” so that the shape possesses vertical and horizontal symmetry. For example, using exactly thiry-two square tiles we can form two different square lamina.
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae.
Using up to one million tiles how many different square laminae can be formed?
To count the different ways, we can keep the distance between the hole and the larger side constant, and count how many laminae can be made with that distance. In the first square in the example, the distance between the hole and the side is 2, while in the 2nd square, the distance is 1.
If we keep the distance constant, we will vary the size of the hole. Given the hole side length $s_h$ and the distance to the side as $k$, the number of tiles needed is difference in areas. The hole area is $s_h^2$, while the area of the larger square is $(s_h+2k)^2$. \[(s_h+2k)^2-s_h^2=s_h^2+4ks_h+4k^2-s_h^2 = 4k(s_h+k)\]
Since we are keeping $k$ constant, we want to see what the maximum hole size would be. If we are allowed a max of $T$ tiles, then the maximum hole size is \[\begin{aligned} 4k(s_h+k) &\leq T \\ s_h+k &\leq \frac{T}{4k} \\ s_h &\leq \frac{T}{4k}-k \end{aligned}\]
Therefore, for each distance $k$, the total number of tilings with that distance is $\lfloor \frac{T}{4k}-k \rfloor$. The maximum distance we can have will occur when the hole size is 1. So we set $s_h=1$ and solve for $k$: \[\begin{aligned} &1 \leq \frac{T}{4k}-k \\ 4k^2+4k-T \leq\, &0 \\ \frac{-4-\sqrt{16-4(4)(-T)}}{8} \leq\, &k \leq \frac{-4+\sqrt{16-4(4)(-T)}}{8} \\ -\frac{\sqrt{T+1}+1}{2} \leq\, &k \leq \frac{\sqrt{T+1}-1}{2} \end{aligned}\]
The left side is negative, so we take the right side. We know have all the pieces required to calculate the number we want.
We simply write a loop from $k=1$ up to $\frac{\sqrt{T+1}-1}{2}$ and add the number of tilings with that distance.
# file: "problem173.py"
T = 10 ** 6
# Maximum distance between
# inner hole and edge
maxK = int(((1 + T) ** 0.5 - 1) / 2)
# For each inner distance, find
# number of tilings possible,
# with number of tiles <= 100
numOfTilings = 0
for k in range(1, maxK + 1):
# The number of tilings with this distance k...
numOfTilings += int(T / (4 * k) - k)
print(numOfTilings)
Or, if you prefer a one-liner:
# file: "problem173.py"
T = 10 ** 6
print(sum(int(T / (4 * k) - k) for k in range(1, int(((1 + T) ** 0.5 - 1) / 2) + 1)))
Running the one-liner code, we have
1572729
0.00018640000000003099 seconds.
Therefore, the number of ways is 1572729.