#139 - Pythagorean tiles
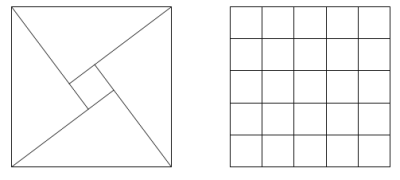
Let $(a,b,c)$ represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length $c$.
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
However, if (5, 12, 13) triangles were used, then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square.
Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
We can use our useful Pythagorean generation technique. We will calculate the size of the hole first. We have a square of side length $c$ with four triangles. Thus, we subtract the area of the 4 triangles from the area of the larger square: \[c^2-4\left(\frac{1}{2}ab\right) = c^2-2ab = a^2+b^2-2ab = (a-b)^2\]
| SquareSquare rooting this expression gets us the side length of $a-b$. Since we don’t know which variable is bigger, we can take the absolute value. **Therefore, this means the triples we are interested are those where $\mathbf{ | a-b | =1}$**. |
Repeatedly appling the $B$ matrix preserves exactly this property. We do not need to run our recursive function, and just keep multiplying by $B$ until we surpass the perimeter threshold.
# file: "problem139.py"
B = np.array([
[1, 2, 2],
[2, 1, 2],
[2, 2, 3]
], dtype=object)
tilings = 0
limit = 100000000
# Only of square 1 can divide...
triple = np.array([3, 4, 5])
while sum(triple) < limit:
print(tilings)
# This has a square of 1.
tilings += limit // sum(triple)
triple = np.dot(B, triple)
print(tilings)
Running this short loop results in an output of,
10057761
0.00013170000000001236 seconds.
Therefore, our final answer is 10057761.