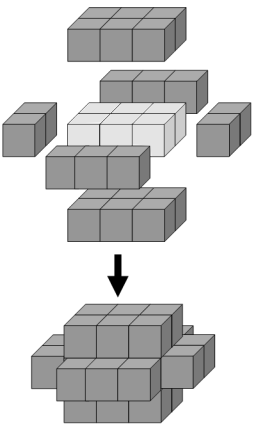
#126 - Cuboid layers
The minimum number of cubes to cover every visible face on a cuboid measuring 3 x 2 x 1 is twenty-two.
If we then add a second layer to the solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, 11 x 1 x 1 all contain forty-six cubes.
We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2, C(46) = 4, C(78) = 5$, and $C(118) = 8$.
It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
Find the least value of $n$ for which $C(n) = 1000$.
We need to find a formula for the number of cubes given the initial dimensions and the layer. Then we need some bounds on the dimensions and layer amounts to perform an exhaustive search.
Formula for the number of cubes
Since we are completely covering the previous layer, the number of cubes will depend on the surface area of the initial cuboid. In the example, the surface area of the $3\times 2\times 1$ cuboid is 22, so we need 22 cubes for this first layer. Calculating the surface area after that is tricky, and the following graphic will help visualize the cubes. he squares marked in blue are where the “surface-area” cubes will lie, and then ones marked on red squares are where the rest will lie. These squares in red are repeated 4 times throughout the cuboid, so we multiply by 4 as shown.
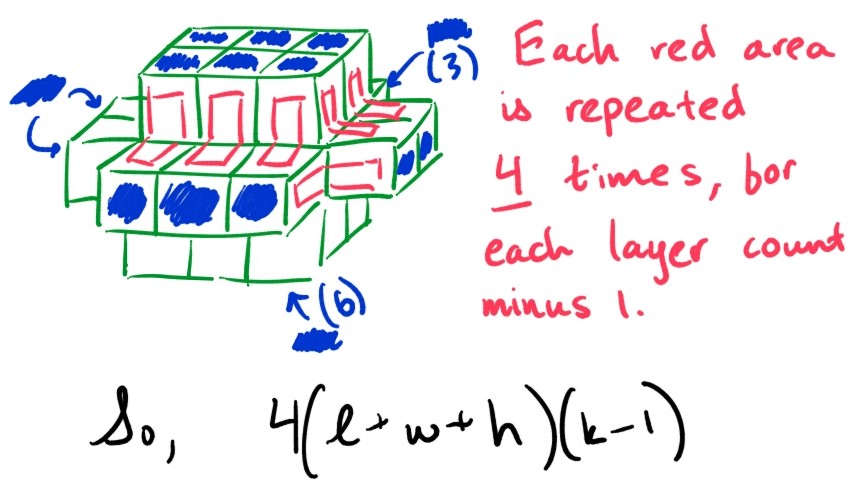
Our formula looks like it should be be $2(\ell w + \ell h+ wh) + 4(\ell + w + h)(k-1)$. This works for $k=1$ and $k=2$. However, when $k=3$, the formula gives 70 cubes, while the actual answer is 78. The undercounting only grows as $k$ grows.
Extra cubes
From the 3rd layer on, we get extra corner cubes that do not get completely colored. Below, you can see what the second layer looks like. Each stud corresponds to a single cube.

Now, if we were to cover it with the cubes we accounted for using the formula, here is what we cover. Remember, we cover the original shape, and the sides for each previous layer.

Notice the yellow areas left uncovered on each corner? We can cover them with 2 cubes per corner, for a total of 8 cubes, which is exactly how many we were short. Just like how we have a $k-1$ factor for covering the steps, we have the same factor here because each time a layer gets added, an extra corner piece has to be added to be compensated. This, coupled with the fact these start appearing from the 3rd layer, means our extra factor is $4(k-2)(k-1)$. We can merge this and the previous factor to get our final formula of, \[Cubes(\ell, w, h, k) = 2(\ell w+\ell h + wh) + 4(\ell + w + h + k - 2)(k-1)\]
Finding $C(n)$
To avoid looking at duplicate cubes, I’ll assume that $\ell\geq w\geq h$. The method will examine all possible cuboid dimensions given the layer. Thus, we will start from the 1st layer, look at all cuboids whose first layer cubes don’t exceed a limit, then move onto the 2nd layer and do the same thing. We keep going until the worst-case cuboid (a 1 x 1 x 1) will exceed the cubes limit on the $k^{\text{th}}$ layer.
To find bounds on the dimensions given the layer, we look at worst-case cuboids. If we leave the length to be variable, then in the worst-case, we have $w = h = 1$. If our cubes limit is $N$, then plugging in these values into our equation means we have \[Cubes(\ell, 1, 1, k) = 4k\ell + 4k^2 - 4k + 2 \leq N\]
Solving for $\ell$, we get that
\(\ell\leq\frac{n-2}{4k}-k+1\) For each value of $\ell$, we constrain the width the same way, by assuming that the worst-case height is 1. The height is similar, only now both values of the length and width is inserted. As you can guess, the equations get more complicated:
\(\begin{aligned} w &= 2 + \frac{2k(k+\ell) - \ell + n/2}{2k+\ell-1} \\ h &= 2 + \frac{2k(1-k-\ell-w)-\ell w + n/2}{2k+\ell+w-2} \end{aligned}\)
Implementation
The code is a deep for-loop, with functions to calculate the upper bounds on the dimensions as well to calculate the number of cubes. I keep a running array of how many times I’ve calculated the same number of cubes. In the end, I find the smallest value where the count is 1000, which is achieved natively through .index(). I also needed some trial and error for the limit.
# file: "problem126.py"
def cubesInKthLayer(l, w, h, k):
return 4 * (k - 1) * (l + w + h + k - 2) + 2 * (l * h + w * h + l * w)
# Function to get maximum L possible given a k and
# number of cubes n
def getMaxL(k, n):
return 1 - k + (n - 2) / (4 * k)
# Function to maximu W possible given k, n, l
def getMaxW(l, k, n):
return 2 + (2 * k * (k + l) - l + n / 2) / (2 * k + l - 1)
# Function to get max H possible given all others...
def getMaxH(l, w, k, n):
return 2 + (2 * k * (1 - k - l - w) - l * w + n / 2) / (2 * k + l + w - 2)
limit = 20000
# Create array of this long which holds
# C(n) for each index...
# Values start with C(1) so
# C(n) = C[n - 1]
C = [0] * limit
# While the kth layer results
# in possible cuboids...
k = 1
L = getMaxL(k, limit)
while L > 1:
# Iterate over each length...
for l in range(1, int(L) + 1):
# Calculate max possible width
W = min(l, getMaxW(l, k, limit))
for w in range(1, int(W) + 1):
H = min(w, getMaxH(l, w, k, limit))
for h in range(1, int(H) + 1):
# Calculate number of cubes
# given the cuboid dimensions and
# layer k. Increment in the array
# by 1.
cuboids = cubesInKthLayer(l, w, h, k)
C[cuboids - 1] += 1
# Move up one layer and recalculate
# maximum possible length
k += 1
L = getMaxL(k, limit)
# We want the first element in
# C which is 1000.
print(C.index(1000) + 1)
The output the program gives us is
18522
2.3773630000650883 seconds.
Thus, the minimum value such that $C(n) = 1000$ is 18522.