#82 - Path sum: three ways

in Project Euler on 20%

This problem is a more challenging version of #81 - Path sum: two ways

The minimal path sum in the 5 by 5 matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to 994. \[\begin{pmatrix} 131 & 673 & \color{red}{\mathbf{234}} & \color{red}{\mathbf{103}} & \color{red}{\mathbf{18}} \\ \color{red}{\mathbf{201}} & \color{red}{\mathbf{96}} & \color{red}{\mathbf{342}} & 965 & 150 \\ 630 & 803 & 746 & 422 & 111 \\ 537 & 699 & 497 & 121 & 956 \\ 805 & 732 & 524 & 37 & 331 \end{pmatrix}\]

Find the minimal path sum from the left column to the right column in matrix.txt (right click and “Save Link/Target As…”), a 31K text file containing an 80 by 80 matrix.

This is a proper step up from #81 - Path sum: two ways, because now we have an extra direction we have to worry about. However, we can still adapt the same concepts to this problem.

Since we’re going column by column, we would update the cells in each colunm to reflect the minimum sum ending in that cell. There is no reason to move up or down when we get to the last column.

To compute the minimum cells in each column, we need another loop to go through all possible paths: 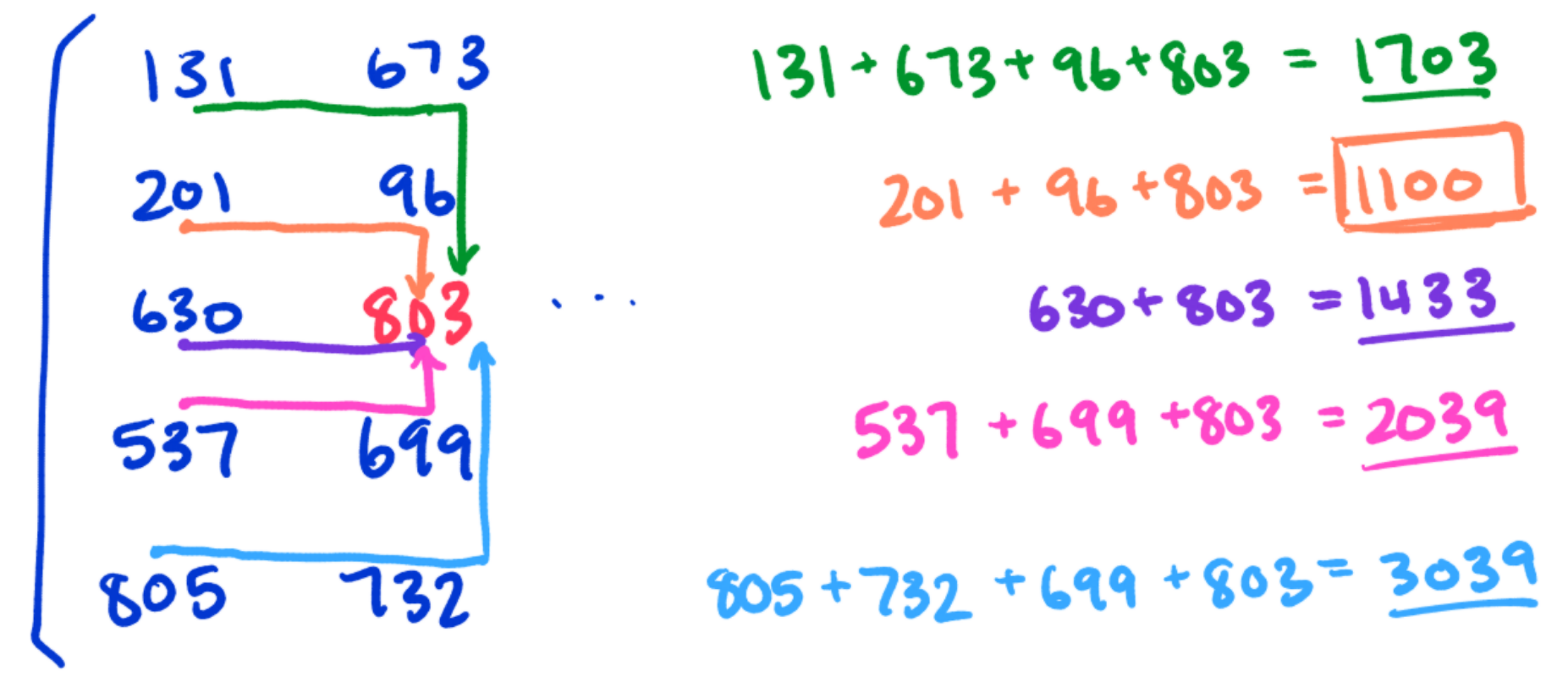sumImage Because we have an extra direction, we are spending a quadratic amount of time in each column, which ultimately leads to a cubic algorithm. This makes intuitive sense, as the two-way problem had a quadratic solution.

The np.cumsum function can quickly calculate the vertical sums.

# file: "problem082.py"
matrix = np.loadtxt('./p082_matrix.txt', dtype='int32', delimiter=',')

# We start on the second column and find the minimum
# sum going from any cell in the previous column to
# that cell. We keep doing this for each column,
# and finally simply add the number directly to
# the right for the second to last column and take the min.

for j in range(1, matrix.shape[1] - 1):
    minSums = np.zeros(matrix.shape[0], dtype='int32')
    for i in range(matrix.shape[0]):
        # Find min of all possible sums coming from the previous column
        # When we come from the bottom (matrix[:i+1,j]) we need to reverse the array...
        minSums[i] = np.min(np.append(np.cumsum(matrix[:i+1, j][::-1]) + matrix[:i+1, j-1][::-1],
                                         np.cumsum(matrix[i:, j]) + matrix[i:, j-1]))

    matrix[:, j] = minSums
# Now just add the last two columns together and take
# the minimum
print(np.min(matrix[:, -2] + matrix[:, -1]))

Running our loop results in an output of,

260324
0.6649046999999999 seconds.

And so, our minimum sum from the left column to the right column is 260324.