#144 - Investigating multiple reflections of a laser beam
In laser physics, a “white cell” is a mirror system that acts as a delay line for the laser beam. The beam enters the cell, bounces around on the mirrors, and eventually works its way back out.
The specific white cell we will be considering is an ellipse with the equation $4x^2+y^2=100$.
The section corresponding to $-0.01\leq x\leq 0.01$ at the top is missing, allowing the light to enter and exit through the hole.
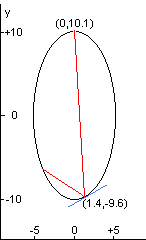
The light beam in this problem starts at the point (0.0, 10.1) just outside the white cell, and the beam first impacts the mirror at (1.4, -9.6).
Each time the laser beam hits the surface of the ellipse, it follows the usual law of reflection “angle of incidence equals angle of reflection.” That is, both the incident and reflected beams make the same angle with the normal line at the point of incidence.
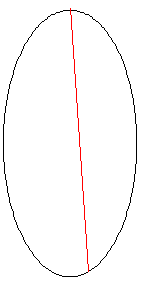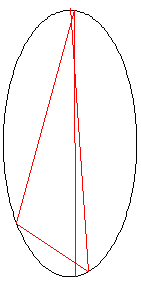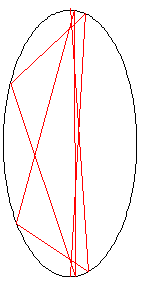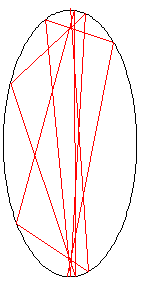
In the figure on the left, the red line shows the first two points of contact between the laser beam and the wall of the white cell; the blue line shows the line tangent to the ellipse at the point of incidence of the first bounce.
The slope $m$ of the tangent line at any point $(x,y)$ of the given ellipse is: $m=-4x/y$.
The normal line is perpendicular to this tangent line at the point of incidence.
The animation on the right shows the first 10 reflections of the beam.
How many times does the beam hit the internal surface of the white cell before exiting?
One term I’ll define: The normal line at a point on the ellipse is the line that is perpendicular to the line tangent to the point. This line will be heavily used, as the laser beam will be reflected across this line. The slopes of two lines that are perpendicular to each other are negative reciprocals of each other.
Two points make a line. A vector and a point also make a line. Since the first two points are given to us, and we know the slope of the normal line, we can reflect the incident laser beam across this line. The reflected laser beam will be pointing in the direction of the next point.
- Find vector associated with incident laser beam.
- Find the normal vector using the slope of the normal line and the reflection point.
- Reflect the incident vector across the normal vector to get the reflected vector.
- Find the equation of the reflected line, and find the other intersection point with the ellipse.
To reflect a vector across another vector, this Math StackExchange answer provides an explanation to the formulas required. If $\mathbf{d}$ is the incident vector and $\hat{\mathbf{n}}$ is the normalized normal vector, then the reflection vector $\mathbf{r}$ is given by \[\mathbf{r} = \mathbf{d} - 2(\mathbf{d}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}}\]
where we use the dot product. Next, we need to find the point where the reflected laser point bounces off of.
Finding the next point
We need the previous two reflection points $(x_0,y_0)$ and $(x_1,y_1)$. Initially, we have $(x_0,y_0) = (0.0, 10.1)$ and $(x_1, y_1)=(1.4,-9.6)$. The vector associated with this line is $\mathbf{v} = \langle x_1-x_0, y_1-y_0 \rangle$.
The normal vector
Next, we need the vector that is normal to the tangent line. Since the slope of the tangent line is $-4x/y$, the slope of the normal line is $y/4x$. Converting to a vector, we have $\mathbf{n}=\langle 4x,y\rangle$. For reflection calculations, we need to normalize this: $\hat{\mathbf{n}}=\frac{\mathbf{n}}{\left\lVert \mathbf{n} \right\rVert}$.
The intersection point
The reflected vector is $\mathbf{r} = \mathbf{v} - 2(\mathbf{v}\cdot\hat{\mathbf{n}})\hat{\mathbf{n}}$. We now convert this vector into its corresponding line equation, so that we can set this equal to the ellipse equation and solve for 2 intersection point. One of these will be the points we just reflected from. We can write the line equation in point-slope form, like so: \[y=m_r(x-x_1)+y_1\]
where $m_r=\frac{r_2}{r_1}$.
We can plug this into the ellipse equation for $y$ directly and with some algebra, we have \[\begin{aligned} 4x^2+y^2 &= 100 \\ 4x^2 + \left(m_r(x-x_1) + y_1\right)^2 &= 100 \\ 4x^2 + m_r^2(x-x_1)^2 + 2m_r(x-x_1)y_1 + y_1^2 &= 100 \\ 4x^2 + m_r^2x^2-2m_r^2xx_1+m_r^2x_1^2+2m_rxy_1-2m_rx_1y_1+y_1^2-100 &= 0 \\ x^2\left[4 + m_r^2\right] + x\left[2m_ry_1-2m_r^2x_1\right] + \left[m_r^2x_1^2 - 2m_rx_1y_1+y_1^2-100\right] &= 0 \\ x_2\big[ 4+m_r^2 \big] + x\big[ 2m_r(y_1-m_rx_1) \big] + \big[ (m_rx_1-y_1)^2-100 \big] &= 0 \end{aligned}\]
Although messy, we have a quadratic equation in $ax^2+bx+c=0$ on the last line, where \[\begin{aligned} a &= 4 + m_r^2 \\ b &= 2m_r\left(y_1-m_rx_1\right) \\ c &= (m_r x_1 - y_1)^2 - 100 \end{aligned}\]
Now plugging into the quadratic formula \[x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
will output two $x$ values. One of these will be the point we just reflected off of, and so we need the other. There isn’t a way to tell which sign we should use, so we have to calculate both and choose. Once we’ve set our $x$, the value of $y$ is given by the normal line equation, and we have our point.
Implementation
The code is just the steps I outlined above in code. To account for possible floating point errors from the square roots, divisions, etc., I used the np.isclose() function.
# file: "problem144.py"
def getNextPoint(p0, p1):
v = p1 - p0
n = np.array([4 * p1[0], p1[1]])
n /= np.linalg.norm(n)
r = v - 2 * np.dot(v, n) * n
# Slope of the reflection line
m = r[1] / r[0]
# Quadratic coefficients
a = 4 + m ** 2
b = 2 * m * (p1[1] - m * p1[0])
c = (p1[0] * m - p1[1]) ** 2 - 100
# Calculate the two solutions...
sols = [(-b - (b * b - 4 * a * c) ** 0.5) / (2 * a), (-b + (b * b - 4 * a * c) ** 0.5) / (2 * a)]
# One of these is original point...
if np.isclose(sols[0], p1[0]):
xNew = sols[1]
else:
xNew = sols[0]
yNew = m * (xNew - p1[0]) + p1[1]
return np.array([xNew, yNew])
p0 = np.array([0, 10.1])
p1 = np.array([1.4, -9.6])
pNew = getNextPoint(p0, p1)
bounces = 1
while np.abs(pNew[0]) > 0.01 or np.abs(10 - pNew[1]) > 0.00002:
pNew = getNextPoint(p0, p1)
bounces += 1
p0 = p1
p1 = pNew
# Due to the while statement, it counted the exit as a "bounce",
# so subtract one...
print(f'The total number bounces inside the cell is {bounces - 1}')
Running, we have
The total number bounces inside the cell is 354.
0.013191799982450902 seconds.
Therefore, the laser beam bounces off the wall 354 times before it exits back through the hole at the top.