#151 - Paper sheets of standard sizes: an expected-value problem
A printing shop runs 16 batches (jobs) every week and each batch requires a sheet of special colour-proofing paper of size A5.
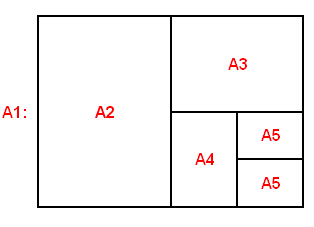
Every Monday morning, the supervisor opens a new envelope, containing a large sheet of the special paper with size A1.
The supervisor proceeds to cut it in half, thus getting two sheets of size A2. Then one of the sheets is cut in half to get two sheets of size A3 and so on until an A5-size sheet is obtained, which is needed for the first batch of the week.
All the unused sheets are placed back in the envelope.
At the beginning of each subsequent batch, the supervisor takes from the envelope one sheet of paper at random. If it is of size A5, then it is used. If it is larger, then the ‘cut-in-half’ procedure is repeated until an A5-size sheet is obtained, and any remaining sheets are always placed back in the envelope.
Excluding the first and last batch of the week, find the expected number of times (during each week) that the supervisor finds a single sheet of paper in the envelope.
Give your answer rounded to six decimal places using the format x.xxxxxx .
From the problem, it should be rare that we find just one piece of paper inside, since we keep cutting in half each time. The quickest way to solve this problem would be a form of brute force. We model all the possible selection paths we can take over the course of the week. For each path, we keep track of the total probability of the path, and the number of times we encountered a single piece of paper. Since these paths are mutually exclusive, we add all probabilities at the end to get the answer.
Each time we cut up a piece of paper, the lower sizes will each go up by one. The A4 produces two A5 pieces, but we use one of them. The probability of selecting a certain size is the count of that size divided by the total number of pieces.
All the states will be stored in one large array, and grows each time with each batch. The state will be represented by 6 numbers. The first 4 are the counts of each size A2 through A5. The 5th number is the probability of encountering at the state at the end of all the batches so far. The last number is the number of times we encountered a single piece of paper during the week.
# file: "problem151.py"
states = np.array([[1, 1, 1, 1, 1, 0]], dtype=float) # 4 states, prob, whether or not the path had 1 paper
batches = 16
totalLeaves = 0
for currBatch in range(2, batches):
numberOfNextStates = np.count_nonzero(states[:, :4])
nextStates = np.empty((numberOfNextStates, 6), dtype=float)
i = 0
for state in states:
# Calculate the probabilities of choosing each size
papProbs = state[:4] / np.sum(state[:4])
for papInd in range(4):
# Skip the sizes which don't have pieces
if state[papInd] == 0:
continue
nextStates[i] = state
# Cut up the paper, that count goes down by 1
nextStates[i, papInd] -= 1
# Each of the lower sizes increases by 1
nextStates[i, papInd + 1:4] += 1
# Multiply the previous state's probability by the probability
# of choosing this size
nextStates[i, 4] = papProbs[papInd] * state[4]
# Copy the encounter flag from last time
nextStates[i, 5] = state[5]
# If this isn't the last batch and we encountered a single sheet,
# then increment the counter
if currBatch < 15 and (np.sum(nextStates[i, :4]) == 1):
nextStates[i, 5] += 1
i += 1
states = nextStates
totalLeaves += len(nextStates)
# Take all the paths which are True and add up those probs
expectation = np.sum(states[:, 4] * states[:, 5])
print('The expected value is', expectation)
Running this nested loop, we get
The expected value is 0.464398781601087
2.0471511000000002 seconds.
Putting it in the format required by the problem, the expected value is 0.464399.