#94 - Almost equilateral triangles
It is easily proved that no equilateral triangle exists with integral length sides and integral area. However, the almost equilateral triangle 5-5-6 has an area of 12 square units.
We shall define an almost equilateral triangle to be a triangle for which two sides are equal and the third differs by no more than one unit.
Find the sum of the perimeters of all almost equilateral triangles with integral side lengths and area and whose perimeters do not exceed one billion (1,000,000,000).
The first question we will tackle is when does an almost equilateral triangle have integral area? From the description, it is clear that almost equilateral triangles are simply isosceles triangles. Finding the area of an isosceles triangle is straightforward. Let $x$ be the base, and $y$ be the two sides that are equal. If you drop a straight line to the base in an isosceles triangle, then it is perpendicular to the base.
The area of our triangle is $\frac{1}{2}x\sqrt{y^2-(x/2)^2}$. This is an integer when $x$ is even and $y^2-(x/2)^2$ is a perfect square. Put another way, if $h$ is our height, it means that $\mathbf{(x/2, h, y)}$ is a Pythagorean triple.
Including our original condition that $x-y = \pm1$, this means that the triples need to have the property that twice the smallest side differs from the hypotenuse by one. Why the smallest side? Because the right triangle that is formed by cutting the isosceles in half has the shorter leg corresponding to our base of the original.
The triples will also be primitive. As we scale up a triple, the difference between them is also scaled i.e. (3, 4, 5) follows our property ($3\times 2 = 6 = 5+1$), but (6, 8, 10) will not, as the difference becomes 2.
To loop through primitive triples, we use the matrices that were first introduced in #39 - Integer right triangles. They have been reproduced below:
\(A=\begin{bmatrix} 1 & -2 & 2 \\ 2 & -1 & 2 \\ 2 & -2 & 3 \end{bmatrix} \\ B=\begin{bmatrix} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 3 \end{bmatrix} \\ C=\begin{bmatrix} -1 & 2 & 2 \\ -2 & 1 & 2 \\ -2 & 2 & 3 \end{bmatrix}\) At each step, you have a choice of 3 matrices to multiply by, and this results in a tree structure.
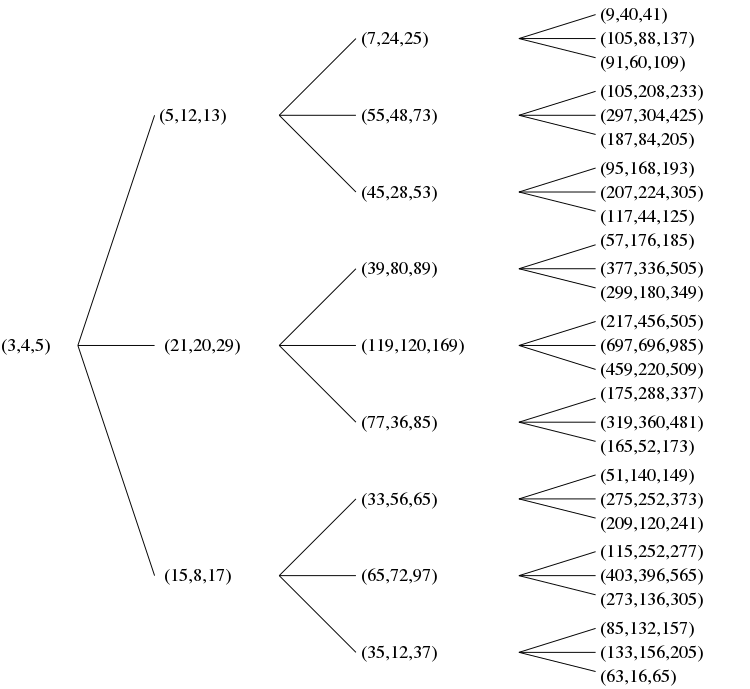Examining the tree, there are only 4 triples that satisfy our desired property:
- $(3,4,5)\rightarrow 3\times 2-5 = 1$
- $(15,8,17)\rightarrow 8\times 2 - 17 = -1$
- $(33,56,65)\rightarrow 33\times 2 - 65 = 1$
- $(209,120,241)\rightarrow 120\times 2 - 241 = -1$
Following the tree, it appears we are alterating multiplying by $A$ and $C$. This is simple to code, as numpy provides us with vector-matrix multiplication.
# file: "problem094.py"
A = np.array([[1, -2, 2], [2, -1, 2], [2, -2, 3]])
C = np.array([[-1, 2, 2], [-2, 1, 2], [-2, 2, 3]])
triple = np.array([3, 4, 5])
Psums = 0
switch = 0 # We need to alternate multiplying A and C, starting with C
while np.sum(triple) <= 1000000000:
perim = 2 * np.max(triple) + 2 * np.min(triple)
# We don't know which one is the minimum,
# so multiply the two numbers which aren't
# the hypotenuse. We have x/2 so no need to
# explicitly divide by 2.
area = np.prod(triple[triple != np.max(triple)])
if not switch:
triple = np.dot(C, triple) # Multiply by C
switch = 1
else:
triple = np.dot(A, triple) # Multiply by A
switch = 0
Psums += perim
print(Psums)
Running this short loop, we get
518408346
0.0014765999999999946 seconds.
Therefore, our final sum of the perimeters is 518408346.
