#107 - Minimal network
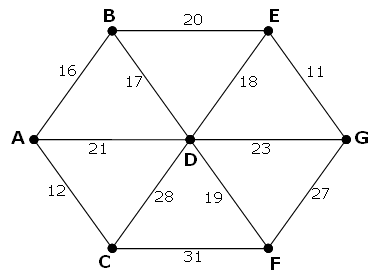
The following undirected network consists of seven vertices and twelve edges with a total weight of 243.
The same network can be represented by the matrix below.
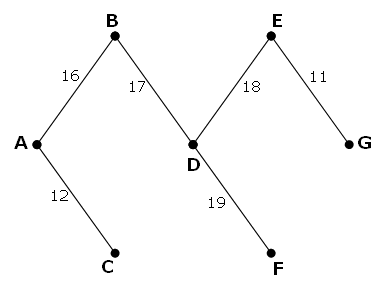
A B C D E F G A - 16 12 21 - - - B 16 - - 17 20 - - C 12 - - 28 - 31 - D 21 17 28 - 18 19 23 E - 20 - 18 - - 11 F - - 31 19 - - 27 G - - - 23 11 27 - However, it is possible to optimise the network by network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of 93, representing a saving of 243 - 93 = 150 from the original network.
Using network.txt (right click and ‘Save Link/Target As…’), a 6K text file containing a network with forty vertices, and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.
The meaning of “connected” is exactly as it sounds like: We don’t have a vertex that’s floating off in space. More specifically, starting from any vertex in the graph, a path exists from it to every other vertex.
Since we want the minimum weight, then that means at each step, find the edge with the largest weight that we can remove such that the graph still remains connected.
What is our stopping condition? We stop when the graph will become disconnected no matter which edge we remove.
Next, how do we test for connectedness given the adjacency matrix? One way is raise to the matrix to a power $k\leq n$ where $n$ is the number of nodes and check for nonzero elements, but that is an expensive operation. Instead, we can run a search through the graph, and if the search results in all the nodes being visited, we have a connected graph.
We will utilize breadth-first-search, which is an iterative search and works very well with an adjacency matrix.
- We start at a node $x$, and then at each loop, we retrieve $x$’s neighbors, and filter them out based on which nodes we haven’t visited yet.
- Then, the next loop will retrieve $x$’s neighbors’ neighbors, and its neighbors, and so on.
- We iterate until there are no new neighbors we can visit. At this point, we look at the set of nodes we haven’t visited.
- If this set is not empty then there are a set of nodes which are unreachable from the node we started at, which means the graph is not connected.
- If the set is empty, then all nodes were able to be visited from the start node, and so the graph is connected.
We are set to write our function. The file that is provided to us contains dashes (“-“) to represent non-existant edges, and I replace these with 0 in the code. Assuming missing edges are 0, then the is_connected() function is straightforward.
Below is the function to see if the graph is connected or not. I assume that the nodes are 0, 1, 2, …, $n$, and we start at node 0. I also use set() objects for quick look up and easy subtraction.
# file: "problem107.py"
def is_connected(graph):
# Does a BFS on the graph. Start at index 0
nodes = len(graph)
start_node = 0
new_neighbors = set(i for i in range(nodes) if graph[start_node][i] != 0)
unvisited = set(range(nodes)) - new_neighbors
# While we are still finding new neighbors, keep getting the next new neighbors
# and updating the unvisited set.
while len(new_neighbors) > 0:
# Only save the neighbors that we haven't visited yet.
new_neighbors = set(i for node in new_neighbors for i in range(nodes) if (graph[node][i] != 0) and i in unvisited)
# Update unvisited set
unvisited -= new_neighbors
# We keep looping as long as we encounter new neighbors, if
# we don't encounter any, but we still have nodes in the unvisited set,
# then the graph is disjoint.
if len(unvisited) > 0:
return False
return True
Now we just retrieve the set of all edges, sorted from largest to smallest weight, and attempt removal of each one. Arrays are copied by reference during equality, so I utilize copy.deepcopy() which creates a full new matrix object. Removal of the edge constitutes setting that edge’s weight to 0 (it’s in two places in the matrix, since the graph is undirected).
# file: "problem107.py"
import copy
with open('./p107_network.txt', 'r') as f:
graph = [line.split(',') for line in f.read().splitlines()]
# Convert the numbers to integers, and convert hyphens to 0
graph = [[int(weight) if weight != '-' else 0 for weight in node_adj_list]for node_adj_list in graph]
# We need a sorted list of edges from largest to smallest,
# as well as their locations. An adjacency matrix is symmetric,
# so make sure not to add edges twice.
edge_locs = [(i, j, graph[i][j]) for i in range(len(graph)) for j in range(i) if graph[i][j] != 0]
edge_locs = sorted(edge_locs, key=lambda x: -x[2])
# Save the current total weight
orig_weight = sum(weight for _, _, weight in edge_locs)
idx = 0
while idx < len(edge_locs):
i, j, weight = edge_locs[idx]
# Check if the graph is connected if this edge is removed,
# so copy the graph.
graph_copy = copy.deepcopy(graph)
graph_copy[i][j] = 0
graph_copy[j][i] = 0 # Symmetric!
if is_connected(graph_copy):
graph = graph_copy
# Delete the edge
del edge_locs[idx]
else:
idx += 1
# Calculate total weight and subtract from original
total_weight = sum(weight for _, _, weight in edge_locs)
print(orig_weight - total_weight)
Running our loop, we get
259679
0.31301869999151677 seconds.
which means our total graph savings is 259679.