All square roots are periodic when written as continued fractions and can be written in the form: \[\sqrt{N}=a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3+\dots}}}\]
For example, let us consider $\sqrt{23}$: \[\sqrt{23}=4+\sqrt{23}-4=4 + \frac{1}{\frac{1}{\sqrt{23} - 4}} = 4 + \frac{1}{1 + \frac{\sqrt{23} - 3}{7}}\]
If we continue we would get the following expansion: \[\sqrt{23} = 4 + \frac{1}{1 + \frac{1}{3 + \frac{1}{1 + \frac{1}{8 + \dots}}}}\]
The process can be summarized as follows: \[\begin{aligned} a_0 &= 4, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23} + 4}{7} = 1 + \frac{\sqrt{23} - 3}{7} \\ a_1 &= 1, \frac{7}{\sqrt{23}-3} = \frac{7(\sqrt{23} + 3)}{14} = 3 + \frac{\sqrt{23} - 3}{2} \\ a_2 &= 3, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23} + 4}{7} = 1 + \frac{\sqrt{23} - 3}{7} \\ a_3 &= 1, \frac{7}{\sqrt{23}-4} = \frac{7(\sqrt{23} + 4)}{7} = 8 + \sqrt{23} - 4 \\ a_4 &= 8, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23} + 4}{7} = 1 + \frac{\sqrt{23} - 3}{7} \\ a_5 &= 1, \frac{7}{\sqrt{23}-3} = \frac{7(\sqrt{23} + 3)}{14} = 3 + \frac{\sqrt{23} - 3}{2} \\ a_6 &= 3, \frac{1}{\sqrt{23}-4} = \frac{\sqrt{23} + 4}{7} = 1 + \frac{\sqrt{23} - 3}{7} \\ a_7 &= 1, \frac{7}{\sqrt{23}-4} = \frac{7(\sqrt{23} + 4)}{7} = 8 + \sqrt{23} - 4 \end{aligned}\]
It can be seen that the sequence is repeating. For conciseness, we use the notation $\sqrt{23}=[4;(1,3,1,8)]$, to indicate that the block (1,3,1,8) repeats indefinitely.
The first ten continued fraction representation of (irrational) square roots are: \[\begin{aligned} \sqrt{2} &= [1;(2)], \text{period=1} \\ \sqrt{3} &= [1:(1,2)], \text{period=2} \\ \sqrt{5} &= [2;(4)], \text{period=1} \\ \sqrt{6} &= [2;(2,4)], \text{period=2} \\ \sqrt{7} &= [2;(1,1,1,4)], \text{period=4} \\ \sqrt{8} &= [2;(1,4)], \text{period=2} \\ \sqrt{10} &= [3;(6)], \text{period=1} \\ \sqrt{11} &= [3;(3,6)], \text{period=2} \\ \sqrt{12} &= [3;(2,6)], \text{period=2} \\ \sqrt{13} &= [3;(1,1,1,1,6)], \text{period=5} \end{aligned}\]
Exactly four continued fractions, for $N\leq 13$, have an odd period.
How many continued fractions for $N\leq10\,000$ have an odd period?
In the card game poker, a hand consists of five cards and are ranked, from lowest to highest, in the following way:
- High Card: Highest value card.
- One Pair: Two cards of the same value.
- Two Pairs: Two different pairs.
- Three of a Kind: Three cards of the same value.
- Straight: All cards are consecutive values.
- Flush: All cards of the same suit.
- Full House: Three of a kind and a pair.
- Four of a Kind: Four cards of the same value.
- Straight Flush: All cards are consecutive values of the same suit.
- Royal Flush: Ten, Jack, Queen, King, Ace, in same suit.
The cards are valued in the order: 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.
If two players have the same ranked hands then the rank made up of the highest value wins; for example, a pair of eights beats a pair of fives (see example 1 below). But if two ranks tie, for example, both players have a pair of queens, then highest cards in each hand are compared (see example 4 below); if the highest cards tie then the next highest cards are compared, and so on.
Consider the following 5 hands dealt to two players:
| Hand | Player 1 | Player 2 | Winner |
|---|
| 1 | 5H 5C 6S 7S KD
Pair of Fives | 2C 3S 8S 8D TD
Pair of Eights | Player 2 |
| 2 | 5D 8C 9S JS AC
Highest card Ace | 2C 5C 7D 8S QH
Highest card Queen | Player 1 |
| 3 | 2D 9C AS AH AC
Three Aces | 3D 6D 7D TD QD
Flush with Diamonds | Player 2 |
| 4 | 4D 6S 9H QH QC
Pair of Queens
Highest card Nine | 3D 6D 7H QD QS
Pair of Queens
Highest card Seven | Player 1 |
| 5 | 2H 2D 4C 4D 4S
Full House
with Three Fours | 3C 3D 3S 9S 9D
Full House
with Three Threes | Player 1 |
The file, poker.txt, contains one-thousand random hands dealt to two players. Each line of the file contains ten cards (separated by a single space): the first five are Player 1’s cards and the last five are Player 2’s cards, You can assume that all hands are valid (no invalid characters or repeated cards), each player’s hands are in no specific order, and in each hand there is a clear winner.
How many hands does Player 1 win?
A number chain is created by continuously adding the square of the digits in a number to form a new number until it has been seen before.
For example, \[44\rightarrow 32\rightarrow 13\rightarrow 10\rightarrow\mathbf{1}\rightarrow\mathbf{1} \\ 85\rightarrow\mathbf{89}\rightarrow145\rightarrow 42\rightarrow20 \rightarrow4\rightarrow16\rightarrow37\rightarrow58\rightarrow\mathbf{89}\]
Therefore any chain that arrives at 1 or 89 will become stuck in an endless loop. What is most amazing is that EVERY starting number will eventually arrive at 1 or 89.
How many starting numbers below ten million will arrive at 89?
The prime 41, can be written as the sum of six consecutive primes: \[41=2+3+5+7+11+13\]
This is the longest sum of consecutive primes that adds to a prime below one-hundred.
The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.
Which prime, below one-million, can be written as the sum of the most consecutive primes?
Note that we are looking for the longest sum, not the largest sum. Therefore, since we can generate a list of primes, we will start at 2, and keep adding terms consecutively. If we reach a prime, then we update the length of the sum. We keep going until our sum exceeds 1 million. Once we’re done starting our sum from 2, we then move to starting the sum with 3. However, since we have saved the longest sum length so far, we have to add that many terms i.e. If the longest sum starting with 2 is 200 digits long, then we start checking sums starting from 3 from 201 digits onward. Like this, we check through all the primes.
The following undirected network consists of seven vertices and twelve edges with a total weight of 243.
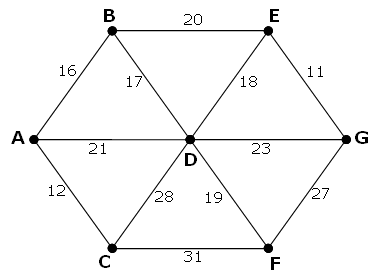
The same network can be represented by the matrix below.
| | A | B | C | D | E | F | G |
|---|
| A | - | 16 | 12 | 21 | - | - | - |
| B | 16 | - | - | 17 | 20 | - | - |
| C | 12 | - | - | 28 | - | 31 | - |
| D | 21 | 17 | 28 | - | 18 | 19 | 23 |
| E | - | 20 | - | 18 | - | - | 11 |
| F | - | - | 31 | 19 | - | - | 27 |
| G | - | - | - | 23 | 11 | 27 | - |
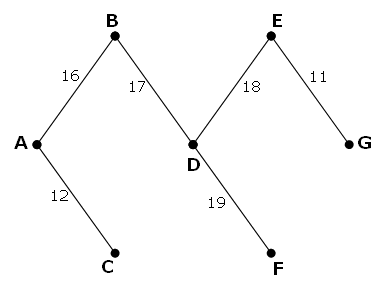
However, it is possible to optimise the network by network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of 93, representing a saving of 243 - 93 = 150 from the original network.
Using network.txt (right click and ‘Save Link/Target As…’), a 6K text file containing a network with forty vertices, and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.
The arithmetic sequence, 1487, 4817, 8147, in which each of the terms increases by 3330, is unusual in two ways: (i) each of the three terms are prime, and, (ii) each of the 4-digit numbers of are permutations of one another.
There are no arithmetic sequences made up 1-, 2-, or 3-digit primes, exhibiting this property, but there is one other 4-digit increasing sequence.
What 12-digit number do you form by concatenating the three terms in this sequence?
The series, $1^1+2^2+3^3+\dots+10^{10}=10405071317$.
Find the last ten digits of the series, $1^1+2^2+3^3+\dots+1000^{1000}$.
The first two consecutive numbers to have two distinct prime factors are: \[\begin{aligned} 14 &= 2\times 7 \\ 15 &= 3\times 5 \end{aligned}\]
The first three consecutive numbers to have three distinct prime factors are: \[\begin{aligned} 644 &= 2^2\times 7\times 23 \\ 645 &= 3\times 5\times 43 \\ 646 &= 2\times 17\times 19 \end{aligned}\]
Find the first four consecutive integers to have four distinct prime factors each. What is the first of these numbers?
It was proposed by Christian Goldbach that every odd composite number that can be written as the sum of a prime and twice a square. \[\begin{aligned} 9 &= 7 + 2\times 1^2 \\ 15 &= 7 + 2\times 2^2 \\ 21 &= 3 + 2\times 3^2 \\ 25 &= 7 + 2\times 3^2 \\ 27 &= 19 + 2\times 2^2 \\ 33 &= 31 + 2\times 1^2 \end{aligned}\]
It turns out that the conjecture was false.
What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?
There are exactly ten ways of selecting three from five, 12345: \[123,\,\,124,\,\,125,\,\,134,\,\,135,\,\,145,\,\,234,\,\,235,\,\,245,\,\,\text{and }345\]
In combinatorics, we use the notation $_5 C_3=10$.
In general $_nC_r=\frac{n!}{r!(n-r)!}$, where $r\leq n, n!=n\times(n-1)\times\dots\times 3\times 2\times 1$, and $0!=1$.
How many, not necessarily distinct, values of $_nC_r$ for $1\leq n\leq 100$, are greater than one-million?


