This problem is a more challenging version of #81 - Path sum: two ways

The minimal path sum in the 5 by 5 matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to 994. \[\begin{pmatrix} 131 & 673 & \color{red}{\mathbf{234}} & \color{red}{\mathbf{103}} & \color{red}{\mathbf{18}} \\ \color{red}{\mathbf{201}} & \color{red}{\mathbf{96}} & \color{red}{\mathbf{342}} & 965 & 150 \\ 630 & 803 & 746 & 422 & 111 \\ 537 & 699 & 497 & 121 & 956 \\ 805 & 732 & 524 & 37 & 331 \end{pmatrix}\]

Find the minimal path sum from the left column to the right column in matrix.txt (right click and “Save Link/Target As…”), a 31K text file containing an 80 by 80 matrix.

The Fibonacci sequence is defined by the recurrence relation: \[F_n=F_{n-1}+F_{n-2} \\ F_1=1 \\ F_2=1\]

It turns out that $F_{541}$, which contains 113 digits, is the first Fibonacci number for which the last nine digits are 1-9 pandigital (contain all the digits 1 to 9, but not necessarily in order). And $F_{2749}$, which contains 575 digits, is the first Fibonacci number for which the first nine digits are 1-9 pandigital.

Given the $F_k$ is the first Fibonacci number for which the first nine digits AND the last nine digits are 1-9 pandigital, find $k$.

Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4. Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.

Peter and Colin roll the dice and compare totals: the highest total wins. The result is a draw if the totals are equal.

What is the probability that Pyramidal Peter beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg

Comparing the two numbres written in index form like $2^{11}$ and $3^7$ is not difficult, as any calculator would confirm that $2^{11}=2048<3^7=2187$.

However, confirming that $632382^{518061}>519432^{525806}$ would be much more difficult, as both numbers contain over three million digits.

Using base_exp.txt (right click and ‘Save Link/Target As…’), a 22K text file containing one thousand lines with a base/exponent pair on each line, determine which line number has the greatest numerical value.

The first two lines in the file represent the numbers in the example given above.

The first known prime found to exceed one million digits was discovered in 1999, and is a Mersenne prime of the form $2^{6972593}-1$; it contains exactly 2,098,960 digits. Subsequently other Mersenne primes, of the form $2^p-1$, have been found which contain more digits.

However, in 2004 there was found a massive non-Mersenne prime which contains 2,357,207 digits: $28433\times2^{7830457}+1$.

Find the last ten digits of this prime number.

If a box contains twenty-one coloured discs, composed of fifteen blue discs and six red discs, and two discs were taken at random, it can be seen that the probability of taking two blue discs $P(BB)=(15/21)\times(14/20)=1/2$.

The next such arrangement, for which there is exactly 50% chance of taking two blue discs at random, is a box containing eighty-five blue discs and thirty-five red discs.

By finding the first arrangement to contain over $10^{12}=1\,000\,000\,000\,000$ discs in total, determine the number of blue discs that the box would contain.

In laser physics, a “white cell” is a mirror system that acts as a delay line for the laser beam. The beam enters the cell, bounces around on the mirrors, and eventually works its way back out.

The specific white cell we will be considering is an ellipse with the equation $4x^2+y^2=100$.

The section corresponding to $-0.01\leq x\leq 0.01$ at the top is missing, allowing the light to enter and exit through the hole.

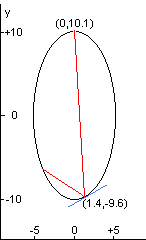
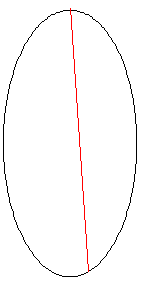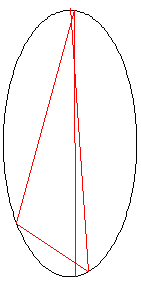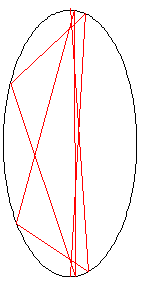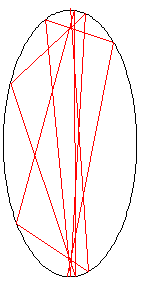
The light beam in this problem starts at the point (0.0, 10.1) just outside the white cell, and the beam first impacts the mirror at (1.4, -9.6).

Each time the laser beam hits the surface of the ellipse, it follows the usual law of reflection “angle of incidence equals angle of reflection.” That is, both the incident and reflected beams make the same angle with the normal line at the point of incidence.

In the figure on the left, the red line shows the first two points of contact between the laser beam and the wall of the white cell; the blue line shows the line tangent to the ellipse at the point of incidence of the first bounce.

The slope $m$ of the tangent line at any point $(x,y)$ of the given ellipse is: $m=-4x/y$.

The normal line is perpendicular to this tangent line at the point of incidence.

The animation on the right shows the first 10 reflections of the beam.

How many times does the beam hit the internal surface of the white cell before exiting?

The 5-digit number, $16807=7^5$, is also a fifth power. Similarly, the 9-digit number, $134\,217\,728=8^9$, is a ninth power.

How many $n$-digit positive integers exist which are also an $n$th power?

The sequence 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201 … is defined by $T_1=1, T_2=1, T_3=1$ and $T_n=T_{n-1}+T_{n-2}+T_{n-3}$.

It can be shown that 27 does not divide any terms of this sequence. In fact, 27 is the first odd number with this property.

Find the 124th odd number that does not divide any number of this sequence.

Consider the fraction, $n/d$, where $n$ and $d$ are positive integers. If $n<d$ and $HCF(n,d)=1$, it is called a reduced proper fraction.

If we list the set of reduced proper fractions for $d\leq 8$ in ascending order of size, we get: \[\frac{1}{8},\frac{1}{7},\frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{2}{7},\frac{1}{3},\mathbf{\frac{3}{8}},\mathbf{\frac{2}{5}}, \mathbf{\frac{3}{7}},\frac{1}{2},\frac{4}{7},\frac{3}{5},\frac{5}{8},\frac{2}{3},\frac{5}{7},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{6}{7},\frac{7}{8}\]

It can be seen that there are 3 fractions between $1/3$ and $1/2$.

How many fractions lie between $1/3$ and $1/2$ in the sorted set of reduced proper fractions for $d\leq12000$?